Nonlinear fit of Mixture distributions

Source: R/fitMixDist.R

This function performs the nonlinear fit of mixture distributions exploiting a firth approach on parameterized finite Gaussian mixture models obtained through the function Mclust from package mclust.

fitMixDist(
  X,
  args = list(norm = c(mean = NA, sd = NA), weibull = c(shape = NA, scale = NA)),
  dens = TRUE,
  npoints = NULL,
  kmean = FALSE,
  maxiter = 1024,
  prior = priorControl(),
  ftol = 1e-14,
  ptol = 1e-14,
  maxfev = 1e+05,
  equalPro = FALSE,
  eps = .Machine$double.eps,
  tol = c(1e-05, sqrt(.Machine$double.eps)),
  usepoints,
  iter.max = 10,
  nstart = 1,
  algorithm = c("Hartigan-Wong", "Lloyd", "Forgy", "MacQueen"),
  seed = 123,
  verbose = TRUE,
  ...
)

Arguments

X

numerical vector. It is user responsability to provide `X` values that belong the definition domain of the functions from mixture distribution.

dens

Logic. Whether to use fit the 'PDF' or 'CDF'. Default is TRUE.

npoints

number of points used in the fit of the density function or NULL. These are used as histogram break points to estimate the empirical density values. If npoints = NULL and dens = TRUE, then. Kernel Density Estimation function density from stats package is used to estimate the empirical density. Default value is 100.

kmean

Logic. Whether to use kmeans algorithm to perform the estimation in place of Mclust. Deafult is FALSE.

maxiter

positive integer. Termination occurs when the number of iterations reaches maxiter. Default value: 1024.

prior

Same as in Mclust function.

ftol

non-negative numeric. Termination occurs when both the actual and predicted relative reductions in the sum of squares are at most ftol. Therefore, ftol measures the relative error desired in the sum of squares. Default value: 1e-12

ptol

non-negative numeric. Termination occurs when the relative error between two consecutive iterates is at most ptol. Therefore, ptol measures the relative error desired in the approximate solution. Default value: 1e-12.

maxfev

Integer; termination occurs when the number of calls to fn has reached maxfev. Note that nls.lm sets the value of maxfev to 100*(length(par) + 1) if maxfev = integer(), where par is the list or vector of parameters to be optimized.

equalPro

An argument to pass to emControl function. Logical variable indicating whether or not the mixing proportions are equal in the model. Default: equalPro = FALSE.

eps, tol

Arguments to pass to emControl function.

usepoints

Integer. Computation by function Mclust could take long time when the sample size is about >= 10000. This number can be used to extract a random sample of size 'usepoints' and to do the estimation with it.

iter.max, nstart, algorithm

Same as in kmeans.

seed

Seed for random number generation.

verbose

if TRUE, prints the function log to stdout and a progress bar

...

Further arguments to pass to other functions like Mclust and density.

arg

A list of named vectors with the corresponding named distribution parameters values. The names of the vector of parameters and the parameter names must correspond to defined functions. For example, if one of the involved distributions is the gamma density (see GammaDist), then the corresponding vector of parameters must be gamma = c(shape = 'some value', scale = 'some value'). For the following distributions, the arguments can be provided with NULL values:

Notice that the distribution given names correspond to the root-names as given for R functions. For example, 'gamma' is the root-name for functions GammaDist. See example, for more details. It is necessary that any the root-name provided corresponds to a defined PDF (if dens = TRUE) or to a defined CDF (if dens = FALSE) found in the session `environment` (see ?environment).

fit.comp

Logical. If FALSE, then starting parameter values for each mixture component will be estimated suing function fitCDF, which could use more computational time. Default is FALSE

Value

A list with the model table with coefficients and goodness-of-fit results, the fitted model returned by function

nls.lm, and a named list of fitted arguments.

Details

The approch tries to fit the proposed mixture distributions using a modification of Levenberg-Marquardt algorithm implemented in function nls.lm from minpack.lm package that is used to perform the nonlinear fit. Cross-validations for the nonlinear regressions (R.Cross.val) are performed as described in reference [1]. In addition, Stein's formula for adjusted R squared (rho) was used as an estimator of the average cross-validation predictive power [1]. Notice that the parameter values must be given in way understandable by the set of functions mixtdistr (see the example below). It is user responsability to provide `X` values that belong the definition domain of the functions from mixture distribution.

References

1. Stevens JP. Applied Multivariate Statistics for the Social Sciences. Fifth Edit. Routledge Academic; 2009.

See also

fitdistr, fitCDF, mixtdistr, and mcgoftest.

Author

Robersy Sanchez (https://genomaths.com).

Examples

#'
set.seed(1) # set a seed for random generation
## ========= A mixture of three distributions =========
phi <- c(6 / 10, 4 / 10) #' Mixture proportions
## ---------------------------------------------------------

## === Named vector of the corresponding distribution function parameters
## must be provided
args <- list(
    gamma = c(shape = 2, scale = 0.1),
    weibull = c(shape = 3, scale = 0.5)
)
## ------------------------------------------------------------

## ===== Sampling from the specified mixture distribution ====
X <- rmixtdistr(n = 1e5, phi = phi, arg = args)
## ------------------------------------------------------------

## ===== Nonlinear fit of the specified mixture distribution ====
FIT <- fitMixDist(X, args = list(
    gamma = c(shape = NA, scale = NA),
    weibull = c(shape = NA, scale = NA)
))
#> fitting ...
#> 
  |                                                                            
  |                                                                      |   0%
  |                                                                            
  |===================================                                   |  50%
  |                                                                            
  |======================================================================| 100%
#> *** Performing nonlinear regression model  crossvalidation...

## === The graphics for the simulated dataset and the corresponding
## theoretical mixture distribution.
par(bg = "gray98", mar = c(3, 4, 2, 1))
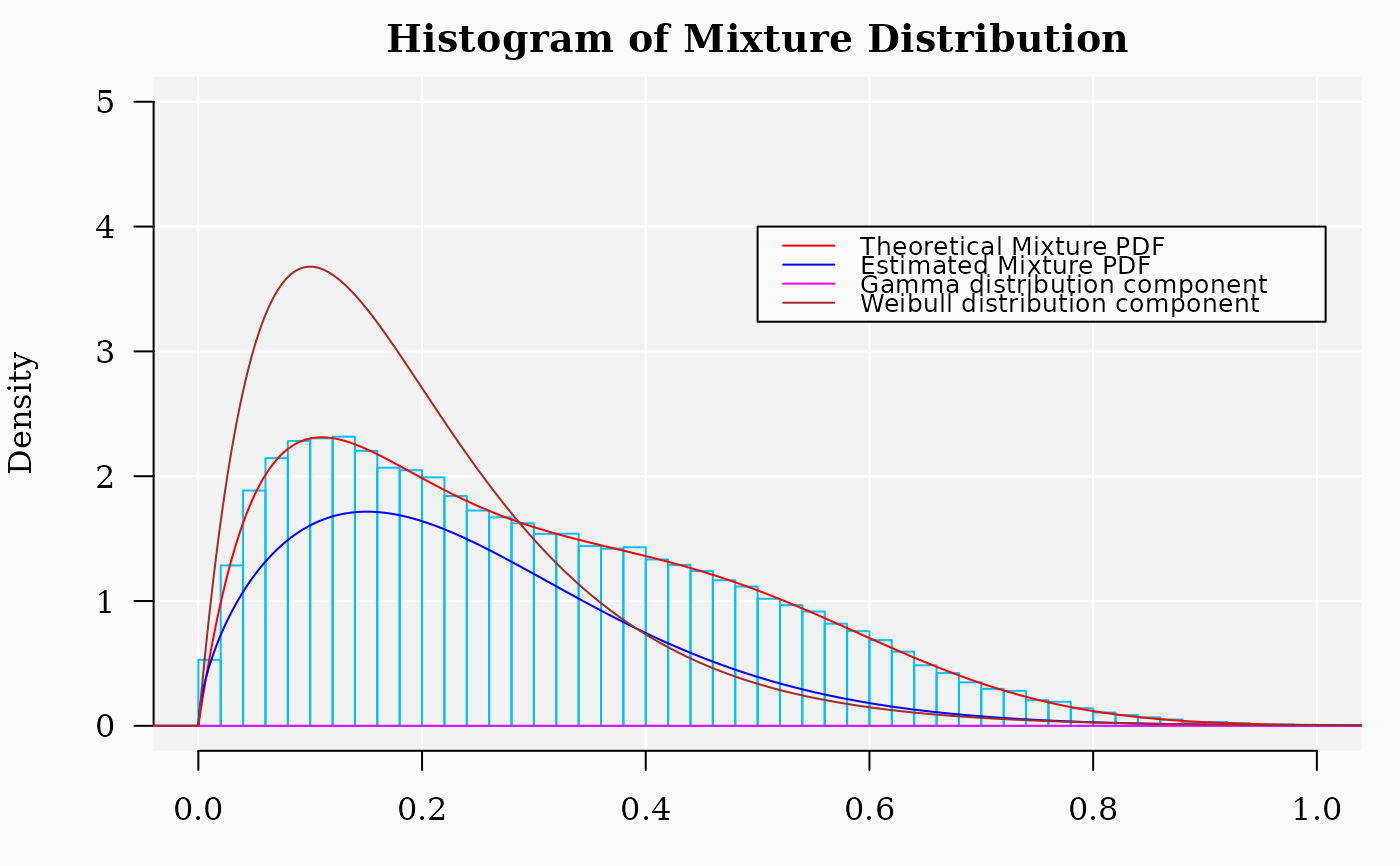
hist(X, 90,
    freq = FALSE, las = 1, ylim = c(0, 5), xlim = c(0, 1),
    panel.first = {
        points(0, 0, pch = 16, cex = 1e6, col = "grey95")
        grid(col = "white", lty = 1)
    },
    family = "serif", col = rgb(0, 0, 1, 0.),
    border = "deepskyblue", main = "Histogram of Mixture Distribution"
)
x1 <- seq(-4, 10, by = 0.001)
lines(x1, dmixtdistr(x1, phi = phi, arg = args), col = "red")
lines(x1, dmixtdistr(x1, phi = FIT$phi, arg = FIT$args), col = "blue")
legend(0.5, 4,
    legend = c(
        "Theoretical Mixture PDF",
        "Estimated Mixture PDF",
        "Gamma distribution component",
        "Weibull distribution component"
    ),
    col = c("red", "blue", "magenta", "brown"), lty = 1, cex = 0.8
)

## The standard definition of dgamma function (see ?dgamma)
lines(x1, dgamma(x1,
    shape = FIT$args$gamma[1],
    scale = FIT$args$gamma[2]
), col = "magenta")
## The standard definition of dgamma function (see ?dgamma)
lines(x1, dgamma(x1,
    shape = args$gamma[1],
    scale = args$gamma[2]
), col = "brown")


## The accuracy of the fitting depends on the the starting values
FIT <- fitMixDist(X, args = list(
    gamma = c(shape = 2.3, scale = 0.12),
    weibull = c(shape = 2.5, scale = 0.4)
))
#> *** Performing nonlinear regression model  crossvalidation...
FIT$args
#> $gamma
#>       shape       scale 
#> 127.5137262   0.0460745 
#> 
#> $weibull
#>    shape    scale 
#> 1.784467 0.231441 
#> 
FIT$phi
#> [1] 0.61701 0.38299